Adaptive Analytics: Predictive Modeling Based on Teachable Skills at UCF

We have recently collaborated with the University of Central Florida and Colorado Technical University on building models that can predict student success at the course level for College Algebra. The journal Current Issues in Emerging eLearning have published our results in the following article:
This blog post summarises a portion of those results. Here we discuss the work carried out at the University of Central Florida, which examined building models based on variables that capture teachable skills. The goal is the possibility of empowering
“… curriculum designers and instructors how to manipulate these analytics variables to engineer student success.”
A second blog post covers the rest of the research results. There we discuss the work carried out on data from Colorado Technical University where we bring time into the model and examine questions such as how early in the course you can get reliable models of success, and what are the most important indicators for student success at various time points in a course.
The Goal
This portion of the study’s primary goal is to find actionable variables that predict student success in the hope that we can create interventions based on these variables. The focus on “actionable” is essential. For example, take GPA. It positively correlates with success, but students arrive with a set GPA. We cannot change it or tell them to come back when it is higher; we have to deal with it as it is. More precisely, as stated in the paper, we wish to
“… address the question of whether or not adaptive learning, with its variable time learning framework, provides a platform for finding actionable analytics variables that predict student success in Algebra and that also are responsive to instruction.”
“The phrase “responsive to instruction” refers to our hope that, if we were able to identify actionable analytics variables that correlate with positive learning outcomes, we also would be able to identify possibilities for teaching curriculum designers and instructors how to manipulate these analytics variables to engineer student success.”
College Algebra at UCF
College Algebra at the UCF requires students to sit for a mathematics placement examination. If they do not meet the department requirement, they must first take a non-credit Intermediate Algebra course. Despite this, at the time of this analysis, nonsuccess in Algebra (a grade of less than C) for students enrolling directly or through IA was approximately 41%. Stated another way, a typical students’ odds of success are favorable but only marginally (about 1.4:1).
The Data
The study used data collected by the Realizeit adaptive learning platform, which provides a wide range of metrics. Our previous work showed that four factors underly these metrics. They broadly measure:
- Knowledge Status
- Knowledge Growth
- Engagement
- Baseline
Please reference the article for more details. When building the model, we focus on the engagement metrics, namely Number of Revisions and Total Time, and are joined by the externally provided student GPA.
The Model
The three variables were converted to quartiles to identify the gain for different cohorts more accurately. This also permitted a more straightforward comparison across cohorts to determine if what we developed would help those in most need by improving their odds of success. Noting the strong influence of GPA on predictions, it played the role of a mediator throughout the analysis - that is, we grouped students by GPA quartile and developed rules for each cohort. GPA quartiles 2 and 3 were not significantly different from each other, so they were combined in the following results.
For each of the three cohorts, we uncovered the same following rule: If students “can obtain a revision placement Q2 through Q4 and a total time of Q4, then their chance of nonsuccess drops.” The rule holds across all cohorts; however, the level of impact varied for each cohort.
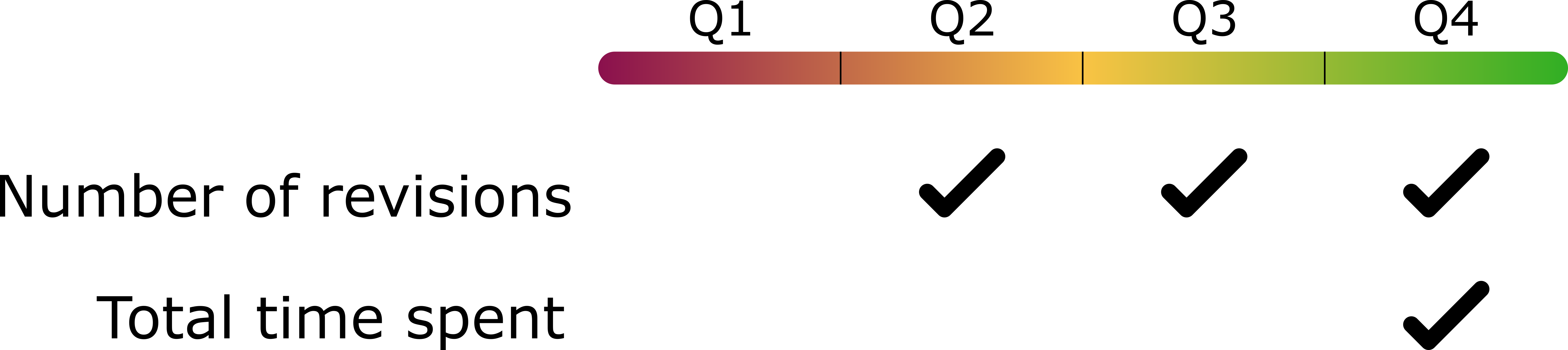
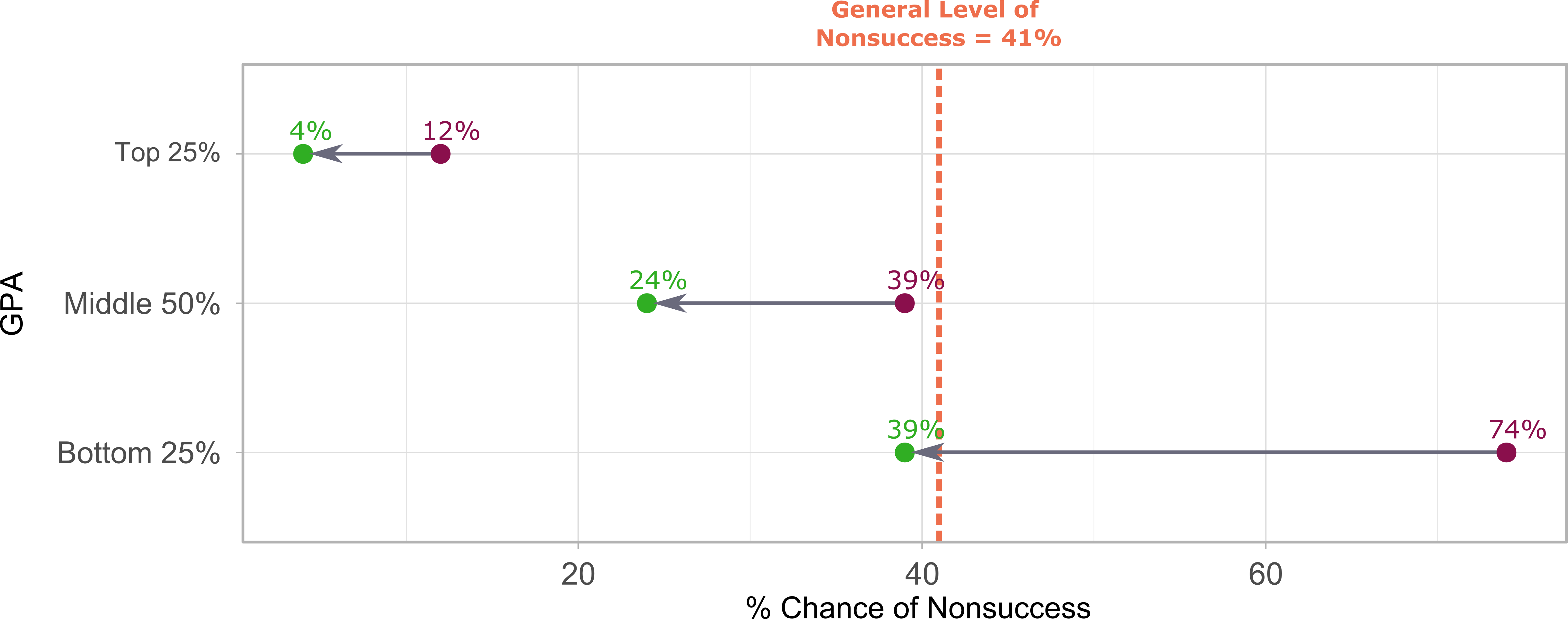
Before we examine each cohort, it is worth remembering that the course’s general level of nonsuccess is 41%. However, this level varies for each of the cohorts. For GPA Q1 (bottom 25%), their level of nonsuccess is 74%, nearly twice the class’s level in general. For GPA Q2 & Q3 (middle 50%), the level is just below the course level at 39%, and for GPA Q4 (top 25%), the level of nonsuccess is just 12%. This last fact is interesting as it shows that while having a high GPA gives a student a great chance of success in College Algebra, it does not guarantee it!
Students who followed the rule and had sufficiently high levels of revision and time spent engaged could dramatically decrease their odds of nonsuccess. For GPA Q1 (bottom 25%), their level of nonsuccess nearly halved, dropping to 39%, just below the class’s level in general. For GPA Q2 & Q3 (middle 50%), the level dropped to 24%, and for GPA Q4 (top 25%), the level of nonsuccess dropped to just 4%. The graphic below summarizes these results.
The key takeaway for an educator is:
“There is a 35% lift for students in GPA Q1, substantially increasing their chance of success. There is a moderate but helpful lift (15%) for students in Q2-Q3 and very little lift for those individuals in Q4 (8%). The rules were most effective for those who needed assistance the most, but, relatively ineffective for those who needed it least.”
So all students can increase their chance of success by revising more and spending more time learning. The students that need the most help benefit the most. This is straightforward guidance to give to students and something that should be easy for them to follow.
Next Up
Read the rest of the research findings in our summary of the work carried out on data from Colorado Technical University, where we bring time into the model and examine questions such as how early in the course you can get reliable models of success, and what are the most important indicators for student success at various time points in a course.
If you found the research article or summary blog posts interesting, please share them with your colleagues!
